Online Automotive Engineering Course
Automotive Design & Marketing Management
5 - AUTOMOBILE MANUFACTURING
We are entering a new phase in the car design and development process. Throughout this automotive course focused on design and marketing we have seen all the stages necessary to have the car fully developed to begin production. This phase is important even for the automotive designer, since it is essential to know how a model is produced and what cost implies any change that you want to make in the design. For example, drawing a car in two tones is extremely easy, but this stylistic detail implies a fork in the production line, in which two lines will run parallel; this supposes an extra cost for the manufacturer. In this phase, engineering becomes very important: in terms of production, industrial organization, supply chain, etc. We're going to see two key elements very summarized: industrial production and logistics, and some very interesting facts about how much it costs to produce a car. How are cars made?Now we are ready to start the production phase. Here we will see how vehicles are made. Before starting to manufacture, two fields come into play:
5 .1- INDUSTRIAL PRODUCTION
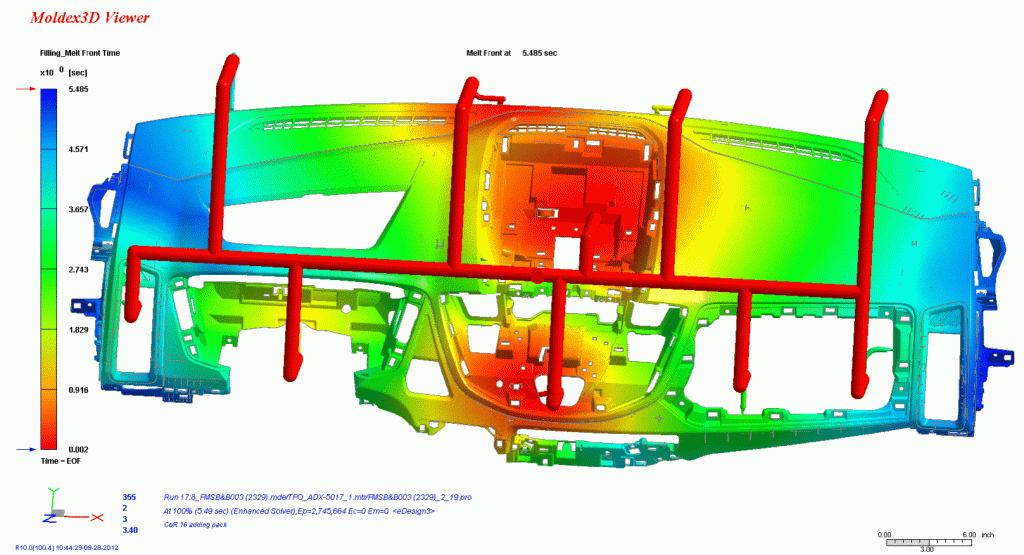
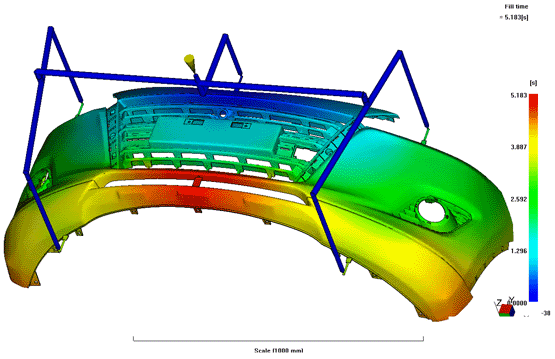
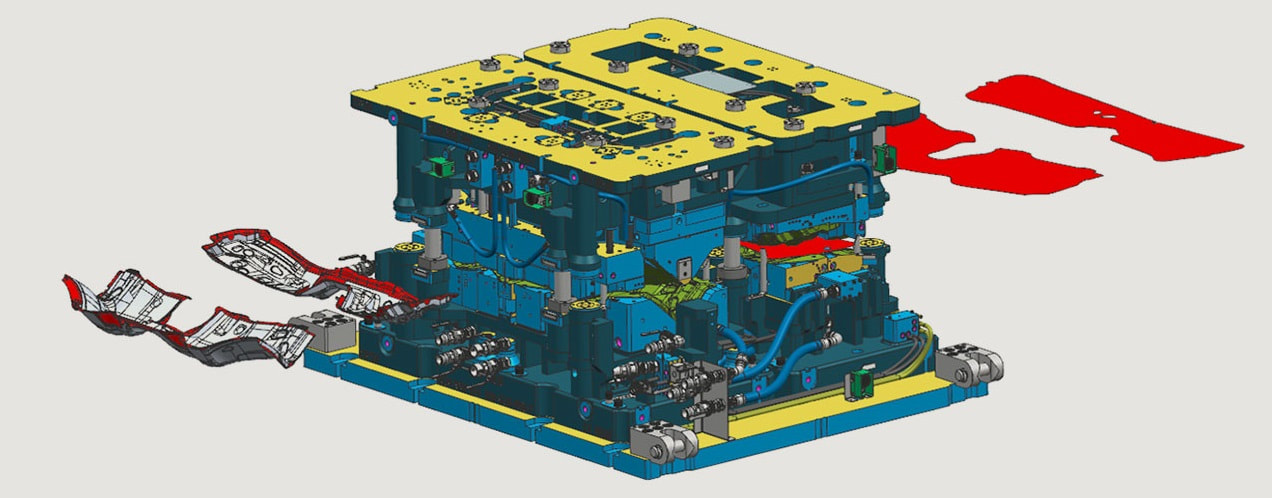
Industrial production of a carThe first step is to design the necessary means for production: dies, molds, fixtures and tools, as well as the production processes and their associated procedures. On this point, the vehicle is fully designed in its final version and we have traveled thousands of kilometers to verify that the car really works. At this point in the design process, it would be awful if a minor change had to be made. Therefore, you have to be totally sure that we have the car in the final version. A minimal variation in a piece can imply the development of new molds that can cost one or two million euros. Theoretically, there should be no further design changes at this point. The design of these molds is also computer-simulated and there is a huge automotive industry specialized in this matter, whether for injection or stamping. Although at this point we will focus on stamping, not plastic injection. The first two images are injection molding simulation and the others are stamping mold design. One must take into account that this phase of automobile development is the highest expression of industrialization. A small change doesn't concern a single vehicle, but thousands of them, which will be sold for years in many countries around the world. This is one of the main differences between a designer and an industrial design engineer. A slight increase in the cost of production would be multiplied by the thousands of units manufactured. Production trial: In this phase the engineers verify that everything has been designed as agreed, and that there are no errors that in the future could be excessively expensive to correct. The engineers then carry out a pre-series production test. At this time, the times are recalculated and adjusted, both in the assembly line and in logistics, under the Just-in-time (JIT) methodology.
5.2- LOGISTICS
Automotive logistics basicsLet's look at the most basic concepts of the logistics of car manufacturing, it really is much more complex. We are going to see two key concepts. The demand for vehicle parts is made under the Just-in-time (JIT) methodology. This work philosophy adjusts the times to the maximum and delivers the pieces just at the moment they are required in order to eliminate, as far as possible, the warehouses. This reduces excess stock, obsolete parts and delivery times; while increasing the speed of production. The deal with the supplier is also improved as it's more continuous, the system is streamlined and allows quick changes in the parts supplied by the Tiers. Due to this, the delay of a single Tier can delay the entire production line, which is why it's so important that everything is perfectly calculated and measured. In the same way, this methodology seeks not to manufacture an excess amount, which is why cars are usually manufactured on demand. The disadvantage of the Just-in-time methodology is that on a day to day there are delays due to weather conditions, human errors, staff losses, etc. It's too risky to compromise a production line with the failure of a single supplier. What are Tier1, tier2, tier3?
All professionals in the sector are familiar with these terms, so it is important to know them.
The Tiers are the suppliers. In the supply chain, a Tier3 provides material to Tier2, and this in turn provides material to Tier1. Therefore, the component manufactured by Tier1 is fed by components manufactured by Tier2, and this in turn by Tier3. In addition to this, we can find the term Tier4 that refers to the raw material. In some countries, Tier3 refers to a mechanical component and Tier2 refers to an electronic component.
BRIEF HISTORICAL INTRODUCTION
Who really invented the production chain?It's known that cars are assembled on an assembly line, but Who invented the assembly line? Allow me a bit of history in this automotive design course; because it wasn't Henry Ford who invented it, even though it appears in countless books. The first assembly line evolved in Venice, in the Arsenal shipyard, it was the most efficient that existed in the Middle Ages. Through a system of channels and walkways, the ship was going through different assembly phases. In this way, one boat was built per day, whereas in other shipyards it took months, so this was a real feat even for today's times. It's believed that it could have been created in the 8th century, but the current structure of the shipyard was established in 1104, in which the ship was gradually manufactured from the keel. In 1320 they built the "Arsenal Nuovo" and improved their serial production system. Almost 150 years later, in 1473, they built the “Arsenal Novissimo” in which up to 16,000 people came to work. It had a production system very similar to the current one. Chain production doesn't derive from the automotive industry but from shipbuilding. So, we already know who invented the production chain, but who transferred it to the automotive industry? Nor was it Henry Ford. So who invented the first automotive production line? The first automotive production line was invented in 1901 by Ransom Eli Olds for the production of his Oldsmobile Curved Dash. Henry Ford improved this system in 1913. In case it is of your interest, as a further reading here you can see which was the first car, it was neither the Cugnot nor the Benz. In fact, the Benz was not even the first gasoline internal combustion car.
HOW MUCH DOES IT COST TO MAKE A CAR?
How much does it cost to make a car?These figures will depend on each manufacturer, we will see in later posts how a car manufacturer makes money. As a general rule, manufacturing costs are around 50% of the final price of the car, excluding taxes. This is distributed in the following way: approximately 42.5% destined only to the materials of the car and the other 7.5% destined to the costs of labor. Labor costs rise for low-volume car brands, which employ more artisan manufacturing, oscillating around 11% of the total car price, excluding taxes. In addition to this, approximately 5.5% of the final price of the car (before taxes) is usually included as depreciation and amortization of the machinery and the rest of the factory materials. This leaves us 55.5% of the production costs of a car. The rest of the costs will be distributed by the marketing, commercial network, guarantees, logistics, design and development of the vehicle, ect. This last point, the design and development of the car usually impacts 6.5% of the final price of the car. This data will give us a great reference to know how much we should invest in the development of our car, if we have previously calculated the sales forecast for the vehicle correctly and we know the final price of the car. In later posts we will see how a car manufacturer makes money and we will see that the profit margins are really low, and sometimes they even lose money for each car made. But now, we will focus on knowing how much it costs to produce a car. Let's make a clarification regarding the amortization of the machinery used to produce the car. We have said that 5.5% of the final price of the car is due to this factor. Most of the parts are subcontracted, sometimes even the assembly of the car itself. In that case the depreciation isn't included because this is already part of the negotiation with the supplier and is already implicit in the final cost of each part. That is, if as a manufacturer I have my own factory and I have thousands of robot arms, I will have to amortize them, and also calculate the depreciation of it. An example with an opposite case: when the manufacture of the metal sheets is outsourced, the car manufacturer doesn't have to calculate the depreciation of the presses as the supplier is responsible for seeing whether or not it's profitable to modify or adjust their machinery. Therefore, the supplier itself will already add its own depreciation to the cost of the metal sheets. This is one of the reasons why the more pieces are produced, the more we can negotiate and lower the unit price. It isn't the same to create a press mold for 100 units than for a million, but that amortization will be the supplier's problem and will impact the final price of the single part. That is, we worry about the amortization of our own machinery, but not the one that the supplier has.
Let's imagine that we decided to build our own vehicle, and we used the same headlights that were used in other models previously, a very common practice especially in low production vehicles.
So, we can negotiate with our supplier a much cheaper price than if they were custom-designed headlights, because the supplier will save design and development costs, but also because it has already amortized the tooling used to manufacture thousands of headlights for another car brand. These details seem insignificant when we have a paper and a pen and we draw a car, but they make the difference between a project becoming a reality or not going beyond sketching. Production costs oscillate over 50% of the final price of the car, in low-volume production vehicles, the cost of labor rises, so it's usual to reduce costs in the parts development to keep that 50%. Furthermore, producing parts exclusively for short runs increases the unit cost excessively. Below we see examples of car models sharing the same headlights.
CAR MANUFACTURING PROCESS
Car Manufacturing ProcessAt this point the engineers have the final design, and it has been proven feasible for production. The factory will be set up with thousands of expensive robot arms, suppliers will be eager to ship their first orders, and if the factory is new, thousands of workers will have found a new job thanks to the car you have designed. The responsibility is enormous, so nothing can go wrong at this point. Knowing this entire process is essential for any automotive engineer.
The phases are divided into the following:
Step 1: Sheet metal pressing
The first step is to obtain the steel that will form the body and other structural components of the vehicle. To do this, the steel is rolled on giant rollers creating a series of sheets of different thicknesses. Usually this step is outsourced, although some large manufacturers control this entire process from start to finish. Once the manufacturer obtains the steel sheets, we go to sheet metal forming in a process called stamping. In the automotive stamping process, the following occurs: A conveyor belt transports the sheets to the press area. Usually, robot arms with suction cups at their ends place the cut metal plate on the conveyor belt, then the press will lower and give the required shape to the piece. As soon as it is finished, another robot arm removes the part towards an exit conveyor belt, while in turn the first robot arm is placing the next sheet to stamp. This movement is perfectly coordinated so that there is no unnecessary waste of time. In this way, the pieces come out at high speed. The press area is also equipped with a set of dies to cut or perforate the part, which can be automatically exchanged. In automotive, the process of changing the dies must be done at high speed. In fact, it's part of the Lean Manufacturing methodology under the so-called SMED, (Single Minute Exchange of Die) in which it's required to change any die or tool in less than ten minutes. This whole process has a complex materials study behind, because stress concentrations occur, and a variation in the properties of the material. Everything is controlled and measured in the design of a vehicle.
Step 2: Body Assembly
Here the car body panels are assembled. The vehicle moves along an assembly line and the robot arms assemble the different parts of the car. In the first sub-phase the fixed parts are assembled and in the second sub-phase the moving parts, such as the doors and the trunk. This part of the process looks like something out of a science fiction movie. Crowd of robot arms performing a perfect choreography, here we can see it on video in a Spanish factory: The level of automation is among the highest that can be seen, whatever the industry. It's about thousands of robots perfectly synchronized to carry out the different tasks with an almost perfect degree of precision. From the beginning of the process, each vehicle is identified to know what stations it will pass through, what paint it will carry and what equipment will be installed. First, the platform is built, that is, the chassis of the vehicle. Different models can share a platform. This is quite common between different manufacturers, that is, that the same platform is used for several models of different brands within the same segment. This produces great economic savings for brands. The chassis moves through the different stations while the car is being formed. After finishing work on one station, the car will move to the next station. So that this flow is constant and there are no stops, the time that the vehicle is in each station will be exactly the same. It's very difficult to design the station and calculate the number of robots and operations to perform. Also, all lines must be parallel. Let us suppose that for the same vehicle there is a version with a roof and another convertible. The production line for the platform is the same, but once we get to the side panels, the line will split in two, as these pieces will be different. Both lines must continue in parallel. Why is this key even in a conceptual design? Because it's really easy to draw a car with several versions, a pickup, another convertible, another with a roof, etc. But in reality, each of these versions represents a new parallel line in the assembly process. In addition, they involve additional molds and new tooling. This fact is well known to design centers. In addition, it's understandable that both versions are not sold equally. For this reason, the initial work that the market research team did is key to being able to size each of these lines. If the marketing team estimates that 90% will be sold with a roof and 10% convertible, it stands to reason that both assembly lines will not have the same workflow. All this must be perfectly calculated and measured by the engineers. After manufacturing the platform, the sides of the vehicle are attached to it, giving rise to the self-supporting chassis. They are usually joined using spot welding, although it can also be done by rivets if the materials are incompatible to be welded. In the case of aluminum, it is done by laser. Then the roof and the lower cross members are mounted. Here we would already have the entire structure of the car assembled, but without any component. Finally, the mobile elements are placed, that is: the doors, the hood and the trunk. There is a robot arm that checks the correct opening of all these elements before moving on to the next phase. At this point the bodywork is called BIW (Body in White), which is when we have the vehicle structure joined and welded, without any assembled element. Some manufacturers, such as RUF and Alpina, start their design and development process at this stage, as they acquire the BIW from Porsche and Bmw respectively. Between phase and phase, different quality controls are carried out to ensure that everything is being manufactured properly. It would not make sense to carry out a single quality check at the end when an error could have been detected at an early stage. What is a robot arm?If you want to work in the automotive industry, you will have to be familiar with robot arms. Even if you work on the conceptual design part, it's always important to know how a car is made. Any factory that mass-produces a vehicle is completely filled with robot arms. These arms are programmed to make very specific movements, but the union of all of them leaves us images as spectacular as those seen in the previous video. These robots can carry as many different components at their ends as you can imagine. In the production line, these arms are usually equipped with different types of manipulators to move the components, such as bases with suckers. They are also equipped with spot welding guns to join the various parts of the body. They are programmed to clean and change the electrodes themselves. Despite their large size, robots are so precise that they are used to verify the exact dimensions of a component or to check that a part is in exactly the correct position. There is an incredible number and variety of robot arms in any industrialized factory, with a multitude of different solutions. Some are only half a meter, but others can be up to six meters tall. But designing a robot arm doesn't just involve programming the coordinates and times. It's also necessary to calculate the dynamics of a robot arm, which is really complex due to its inertial forces. The larger the size of the robot arm, the heavier it will be. Therefore, it will have greater inertia. This will make it more difficult to achieve precision in the final position of each of the movements of the robot arm. That is why larger robots tend to move slower, and also rest a few tenths of a second between each movement. All these small stops are wastes of time, so they must be taken into account. The arms are also designed as light as possible, to minimize the effects of inertia. Similarly, as much mass as possible is transferred to the base of the robot rather than to the end of the arm, to generate lower inertial forces. Artificial intelligence is being implanted in these robots every day, so they don't need programming for each trajectory, but are able to decide which way to go taking into account the environment that surrounds them.
1 Comment
|





























 RSS Feed
RSS Feed